Machine learning for science and engineering
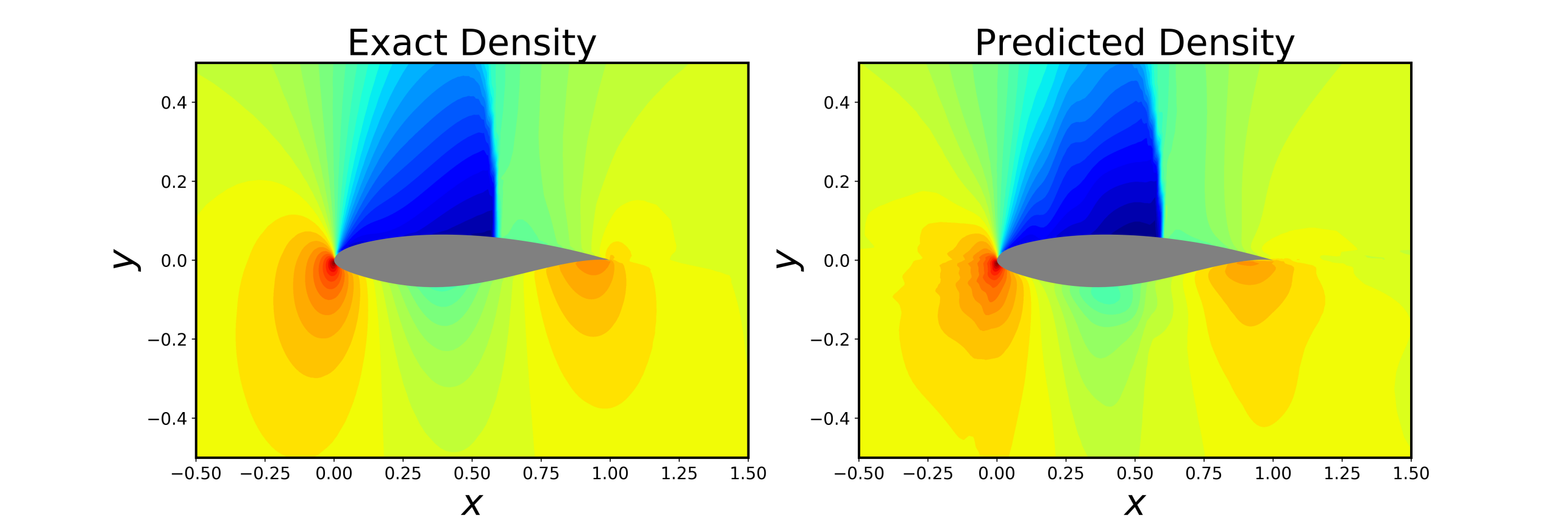
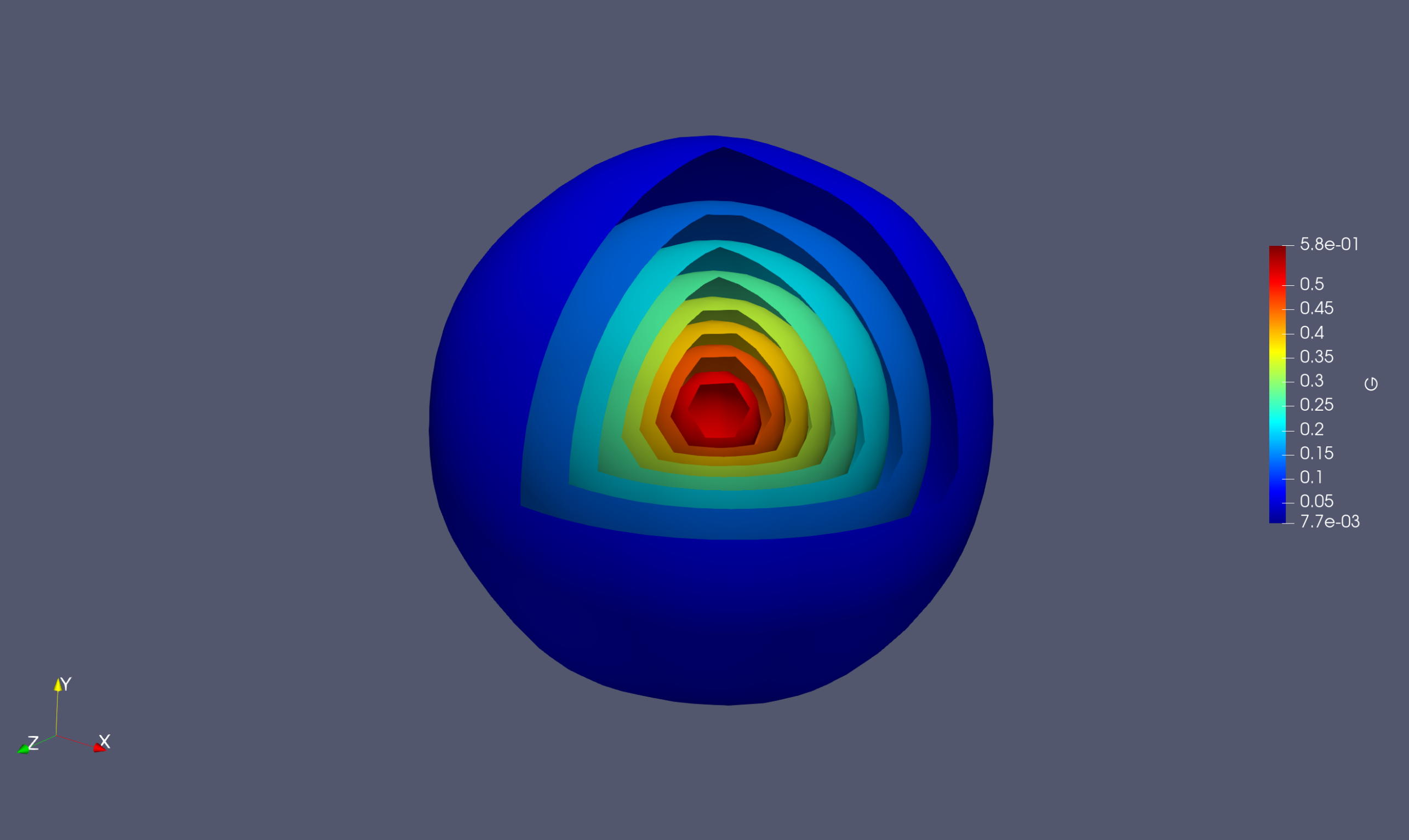
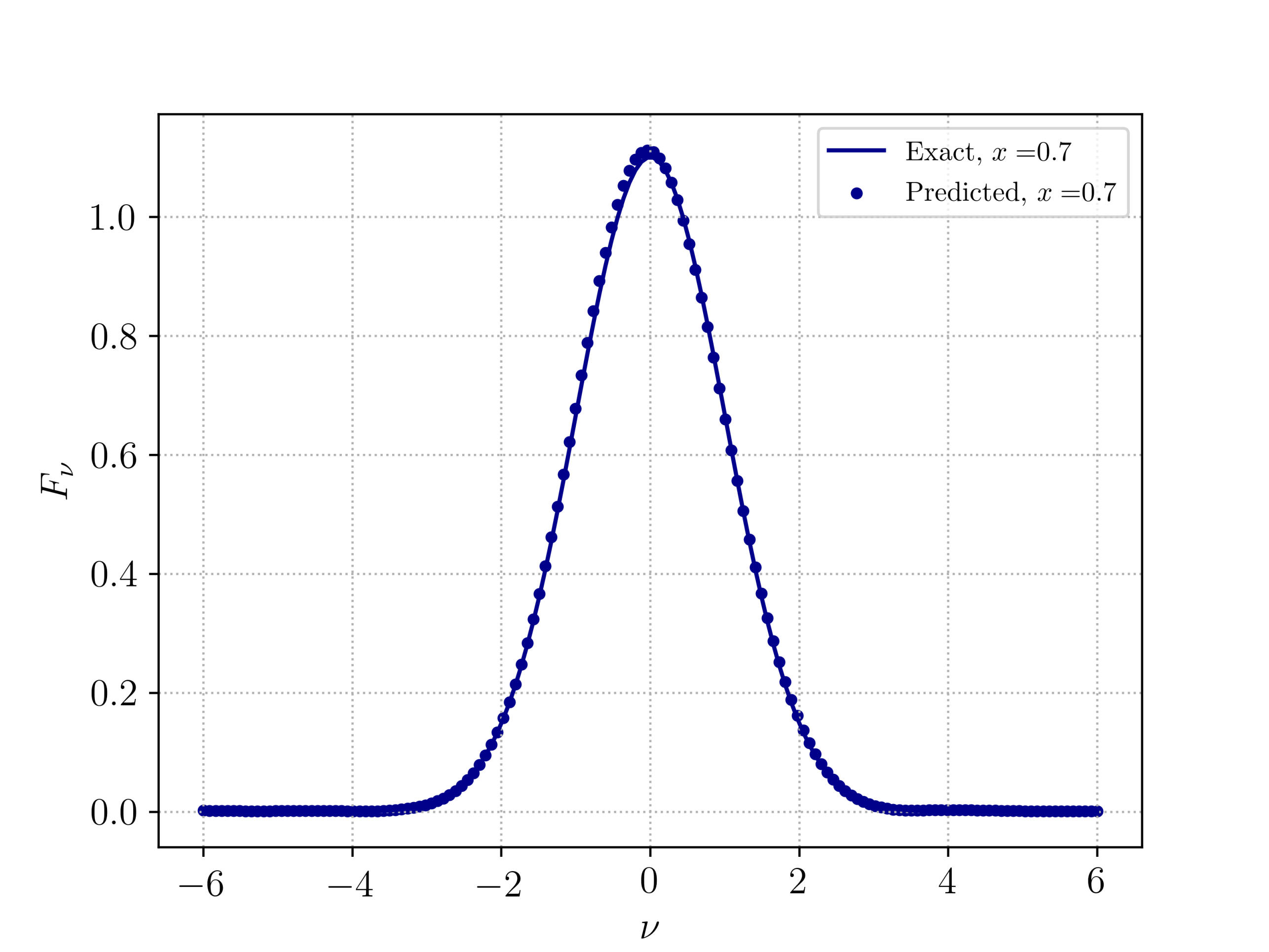
- Learning parameter-to-observables and field maps for solutions of PDEs.
- Physics Informed Neural Networks for forward and inverse problems of PDEs.
- Operator learning for DeepOnets and Fourier Neural Operators (FNOs).
- Applications: surrogate and reduced order modeling, uncertainty quantificaiton, PDEs in very high-dimension, deterministic and Bayesian inverse problems, PDE-constrained optimization and optimial control, data-driven model discovery.
Selected Publications
K. O. Lye, S. Mishra and D. Ray, Deep learning observables incomputational fluid dynamics, J. Comput. Phys.,, 410, 109339, 2020.
I S. Mishra and R. Molinaro, Estimates on the generalization error of physics informed neural networks (PINNs) for approximating PDEs, IMA J. Num. Anal,,, to appear, available from arXiv:2006.16144.
S. Mishra and R. Molinaro, Estimates on the generalization error of physics informed neural networks (PINNs) for approximating a class of inverse problems for PDEs, IMA J. Num. Anal, to appear, available from arXiv:2007.01138.
T. De Ryck and S. Mishra, Error analysis for physics informed neural networks (PINNs) approximating Kolmogorov PDEs, Preprint 2021, arXiv:2106.14473.
S. Lanthaler, S. Mishra and G. E. Karniadakis, Error estimates for DeepOnets: A deep learning framework in infinite dimensions, Preprint 2021. arXiv:2102.09618.
N. Kovachki, S. Lanthaler and S. Mishra, On universal approximation and error bounds for Fourier Neural Operators, J. Machine Learning Research, 22, 2021, 1-76.